Simulado do ENEM
Prova de Mátematica
Questão 1
Uma tubulação despeja sempre o mesmo volume de água por unidade de tempo em uma caixa-d’água, o que significa dizer que a vazão de água nessa tubulação é constante. Na junção dessa tubulação com a caixa-d’água, está instalada uma membrana de filtragem cujo objetivo é filtrar eventuais impurezas presentes na água, combinado a um bom fluxo de água. O fluxo (φ) de água através da superfície da membrana é diretamente proporcional à vazão de água na tubulação, medida em mililitro por segundo, e inversamente proporcional à área da superfície da membrana, medida em centímetro quadrado.
A unidade de medida adequada para descrever o fluxo (φ) de água que atravessa a superfície da membrana é
A
B
C
D
E
Questão 2
Um hospital tem 7 médicos cardiologistas e 6 médicos neurologistas em seu quadro de funcionários. Para executar determinada atividade, a direção desse hospital formará uma equipe com 5 médicos, sendo, pelo menos, 3 cardiologistas.
A
B
C
D
E
Questão 3
Uma professora de matemática utiliza em suas aulas uma “máquina caça-números” para verificar os conhecimentos de seus estudantes sobre representações de números racionais. Essa máquina tem um visor dividido em seis compartimentos e, na lateral, uma alavanca. Cada estudante puxa a alavanca e espera que os compartimentos parem de girar. A partir daí, precisa responder para a professora em quais posições se encontram os números que representam a mesma quantidade.
Um estudante puxou a alavanca, aguardou que os compartimentos parassem de girar e observou os números apresentados no visor. A configuração da máquina naquele instante está apresentada na imagem.
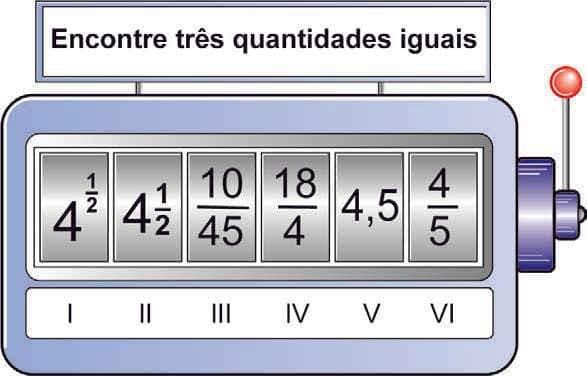
Esse estudante respondeu corretamente à pergunta da professora.
A
I, II e IV.
B
II, IV e V.
C
II, III e V.
D
III, V e VI.
E
III, IV e VI.
Questão 4
João e Felipe participaram, na escola, de uma maratona de matemática na qual, durante uma semana, resolveram 200 questões cada. Nessa maratona, a porcentagem P de acertos de cada participante é convertida em um conceito:
• insatisfatório: se 0 ≤ P < 50;
• regular: se 50 ≤ P < 60;
• bom: se 60 ≤ P < 75;
• muito bom: se 75 ≤ P < 90;
• excelente: se 90 ≤ P ≤ 100.
João acertou 75% das questões da maratona e Felipe acertou 30% a menos que a quantidade de questões que João acertou.
A
muito bom e bom.
B
muito bom e regular.
C
muito bom e insatisfatório.
D
bom e regular.
E
bom e insatisfatório.
Questão 5
Uma empresa de engenharia foi contratada para realizar um serviço no valor de R$ 71250,00. Os sócios da empresa decidiram que 40% desse valor seria destinado ao pagamento de três engenheiros que gerenciaram o serviço. O pagamento para cada um deles será feito de forma diretamente proporcional ao total de horas trabalhadas. O número de dias e o número de horas diárias trabalhadas pelos engenheiros foram, respectivamente:
• engenheiro I: 4 dias, numa jornada de 5 horas e meia por dia;
• engenheiro II: 5 dias, numa jornada de 4 horas por dia;
• engenheiro III: 6 dias, numa jornada de 2 horas e meia por dia.
A
1000
B
1500
C
3500
D
3800
E
5250
Questão 6
Contratos de vários serviços disponíveis na internet apresentam uma quantidade excessiva de informações. Isso faz com que o tempo necessário para a leitura desses contratos possa ser longo.
O quadro apresenta uma amostra do tempo considerado necessário para a leitura completa do contrato de alguns serviços digitais.
A
13,0.
B
15,0.
C
19,8.
D
20,0.
E
23,3.
Questão 7
Uma casa de shows terá um evento cujo custo total de produção é de R$ 34 350,00, sendo que comporta 500 pessoas. O preço do ingresso será de R$ 130,00 e, normalmente, 60% das pessoas adquirem meia-entrada, pagando R$ 65,00 pelo ingresso. Além do faturamento proveniente da venda de ingressos, a casa de shows vende, com 60% de lucro, bebidas e petiscos ao público no dia do evento.
Após ter vendido todos os 500 ingressos, constatou-se que a quantidade de meias-entradas vendidas superou em 50% o que estava previsto, impactando o faturamento estimado com a venda de ingressos.
No dia do evento, decidiu-se manter o percentual de 60% de lucro sobre as bebidas e petiscos, pois todo o público que comprou ingresso compareceu ao show. Com isso, espera-se ter lucro de R$ 17 000,00 nesse evento.
A
19,50.
B
28,80.
C
34,00.
D
52,00.
E
68,70.
Questão 8
Uma empresa tem 400 funcionários, distribuídos em três setores: administrativo, logística e produção. O gráfico apresenta a distribuição quantitativa desses funcionários, por setor e por faixa etária.
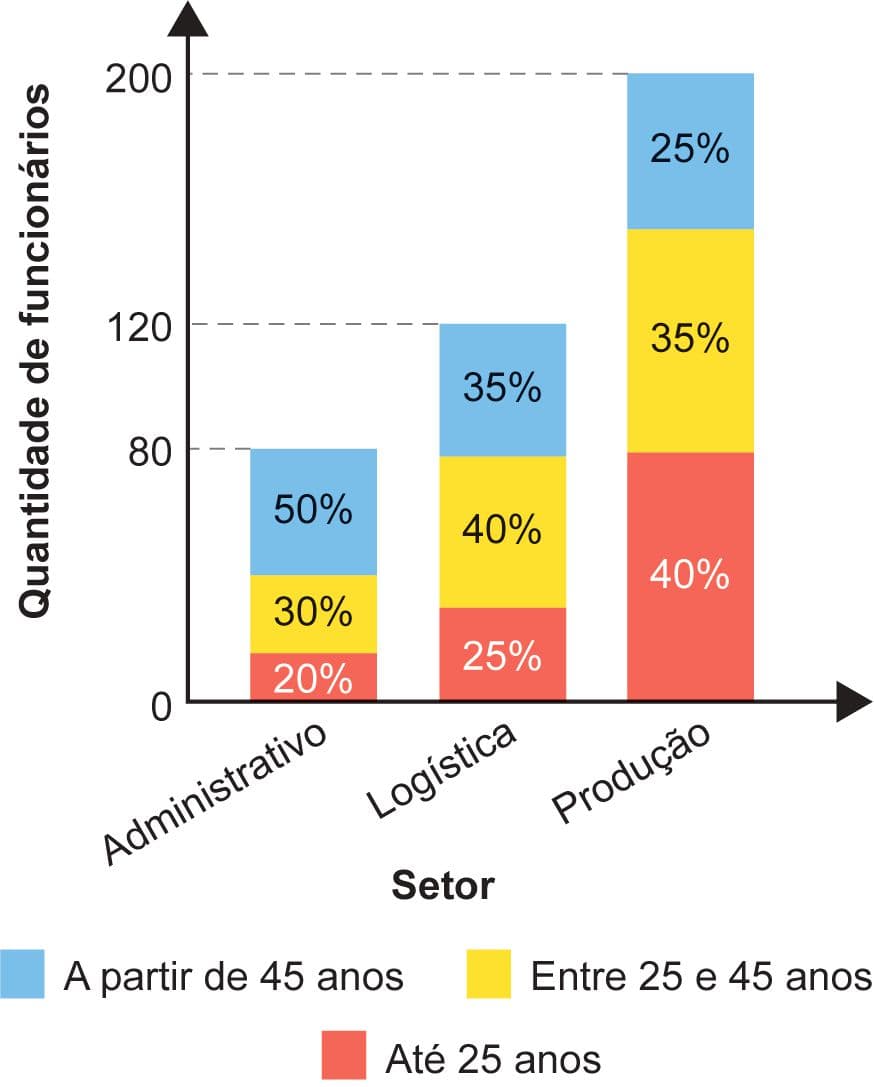
Uma viagem de férias será sorteada entre esses funcionários, de forma que todos terão igual probabilidade de serem sorteados.
A
entre 25 e 45 anos, pois é a faixa etária com maior quantidade de funcionários.
B
entre 25 e 45 anos, pois é a única faixa etária cujas porcentagens são maiores do que as porcentagens mínimas de cada setor.
C
até 25 anos, pois é a única faixa etária cujos percentuais associados aos setores aumentam com o aumento da quantidade de funcionários por setor.
D
até 25 anos, pois é a faixa etária que apresenta maior quantidade de funcionários no setor de produção, que é o setor que emprega metade dos funcionários dessa empresa.
E
a partir de 45 anos, pois a soma das porcentagens associadas a essa faixa etária é 110%, que é maior do que as respectivas somas associadas às outras faixas etárias, que são 105% e 85%.
Questão 9
Um artesão utiliza dois tipos de componentes, X e Y, nos enfeites que produz. Ele sempre compra todos os componentes em uma mesma loja. O quadro apresenta os preços dos dois tipos de componentes nas lojas I e II.
Ele confeccionará enfeites formados por duas unidades do componente X e uma unidade do componente Y e efetuará a compra na loja que oferecer o menor valor total para a confecção de um enfeite.
A
I, pois o valor é R$ 7,00.
B
I, pois o valor é R$ 4,00.
C
II, pois o valor é R$ 6,00.
D
I, pois anuncia o componente com o menor preço.
E
II, pois o componente X, que é o mais utilizado, tem menor preço.
Questão 10
Para melhorar o fluxo de ônibus em uma avenida que tem dois semáforos, a prefeitura reduzirá o tempo em que cada sinal ficará vermelho, que atualmente é de 15 segundos a cada 60 segundos. Admita que o instante de chegada de um ônibus a cada semáforo é aleatório.
O engenheiro de tráfego da prefeitura calculou a probabilidade de um ônibus encontrar cada um deles vermelho, obtendo . A partir daí, estabeleceu uma mesma redução na quantidade do tempo, em segundo, em que cada sinal ficará vermelho, de maneira que a probabilidade de um ônibus encontrar ambos os sinais vermelhos numa mesma viagem seja igual a , considerando os eventos independentes.
Para isso, a redução do tempo em que o sinal ficará vermelho, em segundo, estabelecida pelo engenheiro foi de
A
1,35.
B
3,00.
C
9,00.
D
12,60.
E
13,80.
⏳ Tempo: 30:00
1
2
3
4
5
6
7
8
9
10
Este simulado é apenas uma ferramenta de prática e não substitui a prova oficial do ENEM. Nenhuma pontuação obtida aqui é válida para processos seletivos.
O simulado gratuito baseado nas provas anteriores do ENEM é uma ferramenta gratuita e sem fins lucrativos.